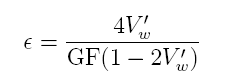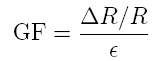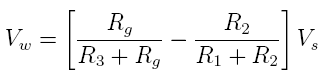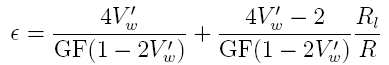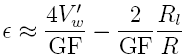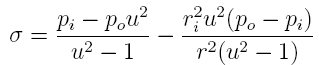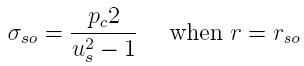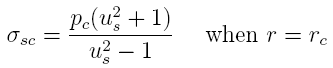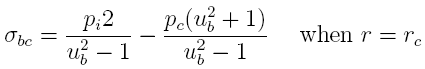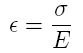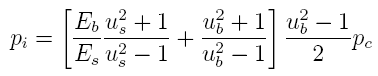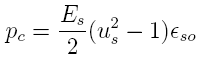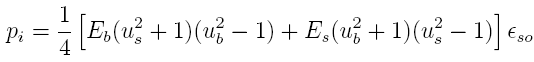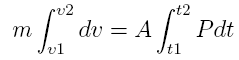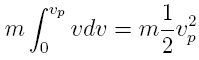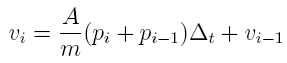Measurement Circuit and Numerical Processing of Chamber
Pressures
by Allen
Dominek and Eddie Dominek
Click here to purchase a
CD with this and all Kitchen Table Gunsmith Articles.
Disclaimer:
This article is for entertainment only and is not to
be used in lieu of a qualified gunsmith.
Please defer all firearms work to a qualified
gunsmith. Any loads
mentioned in this article are my loads for my guns and have
been carefully worked up using established guidelines and
special tools. The
author assumes no responsibility or liability for use of
these loads, or use or misuse of this article.
Please note that I am not a professional gunsmith,
just a shooting enthusiast and hobbyist, as well as a
tinkerer. This
article explains work that I performed to my guns without
the assistance of a qualified gunsmith.
Some procedures described in this article require
special tools and cannot/should not be performed without
them.
Warning:
Disassembling and tinkering with your firearm may
void the warranty. I
claim no responsibility for use or misuse of this article.
Again, this article is for entertainment purposes
only!
Tools
and firearms are the trademark/service mark or registered trademark
of their respective manufacturers. All tools were
purchased from Brownells
unless otherwise indicated.
Note:
Over the past few months I've
had an interesting, ongoing discussion with Allen Dominek
regarding measuring chamber pressure using strain gauges. He
has produced an excellent, and very technical article with
the results of his work and has kindly allowed me to publish
his article here. Enjoy.
Roy Seifert
The Kitchen Table Gunsmith
Introduction
The measurement of gun's
chamber pressure may provide useful diagnostic information
for load design and barrel performance. There are three
measurement techniques involved in chamber pressure
measurements [1,2].
Historically, the standard was a CUP measurement which
captured a peak chamber pressure using a compressible copper
pellet. A more recent technique using a piezo sensor yields
a more accurate measurement of not only peak pressure but of
the pressure in the barrel as the bullet is accelerated.
Both of these methods involve the modification of the gun to
install the sensor. The third technique uses a strain gage
which is placed over the chamber where the round is or at
some other location along the barrel. Hence, such a
measurement technique is non-invasive but not as accurate as
the piezo sensor technique. A strain gage is a small
electrical resistor which is sensitive to small compressive
or expansive forces that the supporting surface experiences.
A potential accuracy limitation does exist from the
analytical formulas used to relate chamber pressure to
strain and the placement of the sensor on the barrel.
Strain gages have been used for many years to measure
deformations. One early study is found here [3].
A commercially available strain sensor system is available
from Recreational Software, Inc. (RSI) [4].
Additional information on sensor preparation and measurement
technique is available at [5].
The
numerical data for the chamber pressure as a function of
time permits additional diagnostic capability. One example
is shown in [6].
Unfortunately, their mathematical derivation for a closed
formula expression relating terminal barrel velocity and
pressure is in error since it assumes a bullet velocity that
is increasing linearly as a function of time. It is this
work that made me interested in chamber pressure
measurements using strain gages.
The
following material outlines my activities for chamber
pressure measurements and numerical processing. The
activities include designing/building the pressure
measurement hardware and numerically processing the measured
data.
Pressure Measurement Hardware
When a round is fired in a
chamber, a complex chemical process (powder burning) occurs
to rapidly build up pressure to accelerate the bullet. This
pressure can be measured using a strain gage attached to the
exterior surface of the chamber since the chamber
approximates an open pressure vessel. There are expressions
relating the interior pressure of a vessel to the expansion
of the vessel. The rifle chamber geometry is not exactly a
traditional pressure vessel but these expressions can be
used to estimate the chamber pressure.
The
key to measuring this pressure is to be able to measure the
strain that the internal pressure exerts upon the barrel. A
strain gage provides an excellent sensor to do this. A
strain gage is an electrical resistor which changes its
resistance due to minute physical geometry changes [7,4,5].
The
measurement of this electric change requires the use of a
Wheatstone bridge. There are a number of different
Wheatstone bridge configurations available [8].
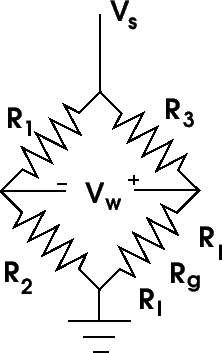
Figure
1 illustrates the typical resistive network. It consists
of three additional resistors with the strain gage.
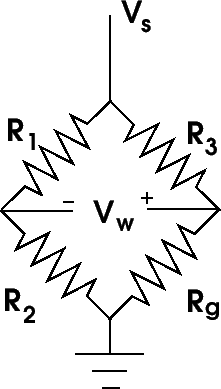
Figure
1: Basic Wheatstone bridge.
When R1/R2 = R3/Rg
the resistance of the sensor changes and this voltage is no
longer zero since the bridge is no longer balanced. It is
this voltage that is measured to obtain the pressure inside
the chamber. The expression which relates voltage to strain
is given in Equation
1 ([8])
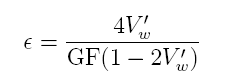
where
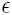 is the strain,
is the strain,
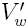 is the normalized measured Wheatstone bridge voltage Vw/Vs
with all the resistors equal R1=R2=R3=R
and Rg=R+∆R. The factor GF is the gage factor
which has a value of around 2. This value is provided by the
gage manufacturer and is the calibration factor for the gage
relating the normalized resistance change to the strain. The
gage factor is defined as
is the normalized measured Wheatstone bridge voltage Vw/Vs
with all the resistors equal R1=R2=R3=R
and Rg=R+∆R. The factor GF is the gage factor
which has a value of around 2. This value is provided by the
gage manufacturer and is the calibration factor for the gage
relating the normalized resistance change to the strain. The
gage factor is defined as
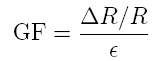
where ∆R is the resistance change of the strain gage.
Equation
1 was derived by expressing the differential voltage as
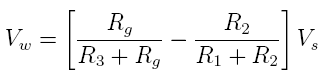
then setting R1=R2=R3=R and
solving for
 using the GF relationship in Equation
2.
using the GF relationship in Equation
2.
When the Wheatstone bridge is physically realized, the
sensor is typically physically removed from the other
resistors and the impact of having connecting wires should
be addressed. Figure
2 illustrates the electrical model.
Figure
2: Wheatstone bridge with sensor wire loss included.
The
effect that the wires present is an additional loss
component. This loss is very small but so is resistance
change of the sensor. Equation
1 can be modified to account for this resistance and is
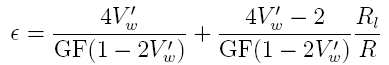
where Rl is the loss in one connecting wire.
In my application, these connecting wires are very short
(~6 inches in length) but still significant with respect
to the resistance change of the sensor as shown later.
For reference, 26 gauge copper wire has about 40
ohms/1000 feet and 30 gauge copper wire has about 100
ohms/1000 feet. Rl to be 0.02 ohms for 6
inches of 26 gauge wire and 0.05 ohms for 6 inches of 30
gauge wire.
Equations
1 and
4 can be simplified since the normalized Wheatstone
bridge voltage is very small. The loss of accuracy has
been numerically confirmed and it is negligible in this
application. The maximum normalized Wheatstone bridge
voltage for a higher power cartridge is of the order of
0.5 millivolt so Equation
4 can be approximated as:
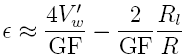
However,
there is probably no reason to use this approximation with
today's numerical calculation resources. It does demonstrate
that the strain is primarily given by the first term and
that the contribution of loss from the connecting wires to
the strain gage is essentially a constant DC term which is
about 100 times smaller than the first term for the given
loss values.
There is a three wire sensor configuration [8]
where a second wire is attached to one of the sensor pads.
This is only effective for eliminating the loss in one of
the wires so I find it not helpful and not really of value
considering the size of Rl in my application.
Pressure/Strain Formulas
The next step is to relate
the measured strain values to the internal pressure of a
chamber. Approximate expressions can be found in [9].
The author attempted to relate the internal chamber pressure
to the external strain on the barrel using expressions for
thick and thin walled pressure vessels. The presentation was
technically weak and resulted in the use of equations not
appropriate for this application. These equations, however,
did provide numerical values that were realistic in
magnitude. A formulation to calculate the internal pressure
of a chamber using measured strain data is presented below.
It is a simple model and appears to be reasonable from the
experimental testing presented later.
Traditional cylindrical pressure vessels are called "open"
or "closed" A person may be tempted to classify a barrel as
a "closed pressure vessel" but it is not. A closed pressure
vessel has axial stresses induced by the internal pressures
of the cylinder since the ends of the cylinder are
physically constrained not to move. Also the classical
"closed pressure vessel" has a steady state pressure
throughout the cylindrical structure.
A
rifle barrel is not a closed pressure vessel in the
classical sense. Both ends are not mechanically constrained.
The muzzle end is free to move. Placing a strain gage
axially along the barrel will not sense any significant
axial deformation when the round is fired. This means that
the barrel can be modeled as an "open pressure vessel".
Additionally, the pressure that the barrel is exposed to is
transient in nature and not steady state (the entire barrel
is not under a uniform pressure). The pressure wave,
generated by firing the round, propagates down the barrel
and does not sense the finiteness of the barrel until the
pressure wave is at the muzzle. Until then, the barrel
appears to be infinitely long. However, when the pressure
wave does reach the muzzle, then additional interaction
occurs. FEM modeling [10]
confirms this simplistic model for early time.
There are a set of equations called Lame equations [11]
describing the stresses in a cylindrical structure when the
internal and external surfaces are under pressure. These
stresses can be grouped into three types: circumferential,
axial and radial. The only stress that is generated or is of
significance when a round is fired in a gun is the
circumferential stress.
The
circumferential stress equation of interest is:
where pi and po are the internal and
external cylinder pressures, u=ro/ri
is the ratio of the outer and inner cylinder diameters and
r is a position between ri and ro.
This equation is appropriate for what is termed "thick wall"
where the cylinder radii are explicitly used.
Equation
6 can be specialized for two geometries, one for the
barrel and one for the casing. In this model, the casing is
in contact with the barrel's inner diameter. Such a geometry
is typically called "compound cylinders". For the barrel,
Equation
6 yields
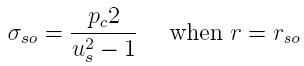
and
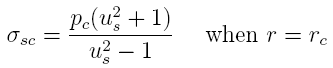
where
Us is the ratio of the outer and inner diameters
of the barrel where the strain gage is located and Pc
is the contact pressure between the ID of the barrel and the
outer diameter of the casing. Equation
9 is the pertinent equation for the casing:
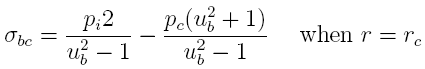
where Pi is the internal pressure in the casing
(barrel) and Ub is the ratio of the outer and
inner diameters of the casing. Note that the subscript "s"
refers to "steel" which is what the barrel is made from and
the subscript "b" refers to "brass" which is what the
cartridge is made from.
The
desired equation to predict the interior pressure in a
barrel by the measured strain on the exterior of a barrel is
derived in two steps. The first step is to relate the change
of circumference at the contact interface between the barrel
and casing when a round is fired. Since both the barrel and
casing are in contact during firing, both have to expand the
same amount. This expansion is governed by the strain at the
interface and has to be continuous at the contact boundary
which requires:
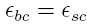
The
strain and stress of a material are related through a
constant call Young's modulus or the modulus of elasticity,
$E$ and is expressed as:
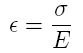
Using
Equations
8 and
9 with Equations
10 and
11 yields:
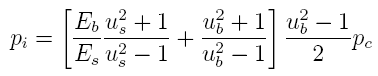
where
the Young's modulus for steel (Es), brass (Eb)
and LDPE (shotgun shells) are 30*10^6, 16*10^6 and
$0.13*10^6 psi, respectively. The contact pressure is
determined by the strain gage reading. Using Equations
7 and
11 yields this contact pressure which is
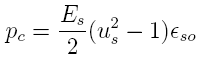
Inserting Pc from Equation
13 into Equation
12 and reducing yields:
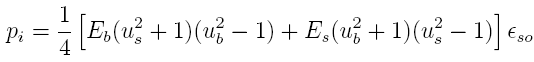
The
accuracy in determining the chamber pressure is dependent
upon many factors. From Equations
4 and
14, the factors are the measured Wheatstone bridge
voltage (dependencies of strain gage bonding/orientation,
the gage factor and amplifier gain), measured chamber/casing
dimensions and the Young's modulus material constants. The
only factors in which there are known uncertainties are the
strain gage bonding quality to the barrel and the Young's
modulus values.
The
dimensions used in Equation
14 should be the dimensions under pressure. Fortunately
for the amount of strain on the barrel, the change of the
barrel dimensions under pressure is negligible. However,
this is not the case for the casing. The outer diameter for
the casing should be the inner diameter of the chamber since
the case is in contact with the barrel during firing. This
results in a thinner case thickness during firing than the
case has under static conditions. The case thickness used in
Equation
14 is scaled from the unfired case thickness. This
scaling is based upon the fact that the amount of brass is
constant. The thickness used is given by t2=r1t1/r2
where the subscripts refer to the dimensions before firing
and 2 refer to the dimensions during firing. The change is
negligible since the casing diameter expands roughly
0.004''.
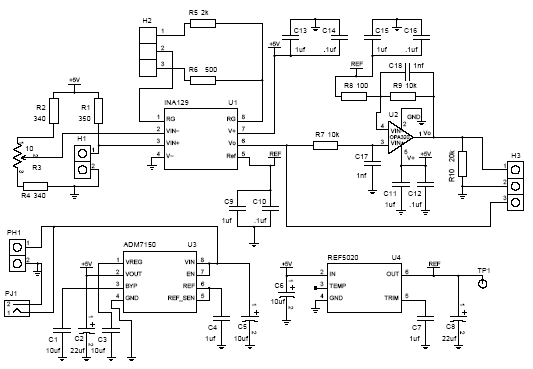
Differential Amplifier Circuit
Modern operational amplifier
(opamp) capabilities allow for very simple circuits to be
made with superior electrical performance. Figure
3 illustrates one circuit that can measure the
differential voltage generated by a Wheatstone bridge. A
Texas Instruments INA129 instrumentation opamp is a device
used to measure and amplify the generated differential
voltage created by the sensor and reject the common mode
voltage of the balanced bridge. The INA129 has the
capability to have an adjustable gain through the resistance
of R5/R6. This is important since
different chambers and loads will have different pressure
maximums. The gain is defined by 1+49.4k/R where R is either
R5 or R6. A gain of 101 is provided
when R6 is 500 ohms and a gain of 26 is provide
when R5 is 2k. Of course, the actual gain should
be measured to obtain the most accurate value for the gain.
The
required gain can be estimated by calculating the expected
pressures and voltages for various guns. The values shown in
Table
1 for a 22LR rifle, a 12 gauge shotgun and a 7mm Mauser
rifle are derived using Equations
12 and
13:
Calculated Wheatstone Voltages
|
Table 1:
|
|
Gun |
us |
pi (kpsi) |
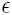 *10^6 (psi)
*10^6 (psi) |
Vw (mV) |
|
22LR |
3.39 |
24 |
130 |
.35 |
|
12 gauge |
1.58 |
10 |
408 |
1.10 |
|
7mm |
2.19 |
48 |
738 |
1.99 |
Each gun requires a different amplifier gain if the maximum
measured voltage is to be the same. The amplifier gains for
the 22LR rifle, 12 gauge shotgun and 7mm rifle are 7100,
2300 and 1300, respectively, if the maximum measured voltage
is 2.5 volts. The current instrumentation opamp has a gain
limit of 10,000 but it is not good practice to use just one
amplifier to achieve large gains. Another stage should be
added. A fixed gain of 100 has been chosen for the second
stage and it will have a low pass filter to attenuate higher
frequency noise. The remaining gain will be provided by the
first stage. A jumper has been provided to choose between
two different gains of 25 and 100. These gains were chosen
before the values in Table
1 were confirmed. A more appropriate set of gains would
be 70, 22 and 12 or less.
All
the components operate on a 5 volt rail supplied by a 9 volt
battery (for portability) and a linear voltage regulator
ADM7150. Opamp REF5020 provides an offset voltage for the
instrumentation opamp output. Since the generated Wheatstone
bridge voltage will be positive (as configured), it is
necessary to offset the opamp output by a small voltage when
the bridge is balanced. This is achieved by offsetting the
INA129 output voltage by 2 volts using REF5020. The gain and
offset voltage should be set so that the maximum output
voltage is less than 4.5 volts for maximum sensitivity.
The
other opamp, an OPA320, provides the remaining gain. The
gain bandwidth product for this opamp is low so when a gain
of 100 is used, the gain naturally rolls off to minimize the
noise at the higher frequencies from being significant. The
roll off starts around 4-5 kHz which is the upper frequency
content limit of the signal of interest to be measured. From
numerical modeling, slightly better noise performance is
achieved when an OPA333 is used instead of an OPA320.
The
circuit uses another multi-turn potentiometer, R3, to
balance the bridge when the sensor has no strain on it. This
adjustment is made to have pin 6 the same voltage as pin 5
on the INA129 opamp when the strain gage is in its nominal
state. I make the adjustment so that the output voltage of
the second stage is the same voltage the reference voltage
provided by REF5020. If this is not done, the amplified
voltage may be railed (at 5 volts) since the gain of the
circuit is quite large.
A
number of connection points (H1, H2, H3 and PH1) are
present. PH1 provides for the connection of the 9v battery.
H1 is the connection point for the strain sensor. H3 is a
measurement point for both the pre-filtered (pin 1) and
filtered (pin 3) amplified voltage. Jumper H2 permits for
two discrete gain values to be chosen for the INA129
amplifier allowing maximum sensitivity depending upon the
peak chamber pressure.
Note that the measured voltage value used in Equation
1 has to be divided by the total gain of the opamp
circuit to recover the Wheatstone bridge voltage.
Numerical Processing
The velocity of the bullet
and its position in the barrel can be estimated once the
pressure in the chamber has been acquired. Note that the
following derivation is under ideal conditions which are not
met in a real life gun chamber/barrel. The calculated
quantities are based upon many assumptions. As previously
mentioned, the measurement and resulting pressure values
have limitations. In this section, no account of all the
energy created by the powder is attempted. Losses include
heating, friction and bullet dynamics.
The
force acting on a bullet is the gas expansion created by the
burning of the powder. Considering Newton's Second Law of
Motion as was done in [6],
the bullet's motion can be roughly modeled by equating its
mass and acceleration to the chamber pressure over its cross
sectional area as
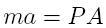
where
m is the mass of the bullet, a is the acceleration, P is the
chamber pressure and A is the area of the bullet. Expanding
the a as the second time derivative of position yields:
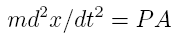
since
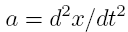
Realizing
that:
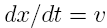
results in Equation
16 becoming:
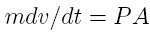
Multiplying both sides with dt and integrating yields:
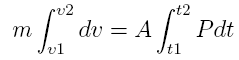
where
v1 and v2 are the velocities of the bullet at times t1 and
t2, respectively. The integration approach used in [6]
is basically wrong. I feel that there is no value in
defining an average pressure as was done and the velocity of
the bullet is not linear so one cannot say that
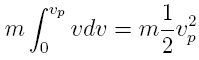
What
can be determined by using Equation
20 is the velocity and position as a function of time by
piece-wise integrating this equation. This is readily
achieved since the measured data would be sampled with
small, uniform temporal spacings. The velocity is determined
by this equation:
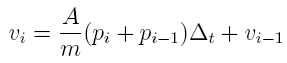
where
∆t=ti-ti-1 and the position is
determine by this equation:
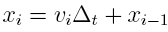
The
initial values for velocity and position are both zero. The
final velocity is the muzzle velocity of when the bullet
exits the barrel and the final position is the length of the
barrel starting from the location of the bullet before it
was fired.
There is one last consideration to make before calculating
velocities and travel distances which is the resistance the
bullet experiences traveling through the barrel. There are
two types of resistance to account for. One resistance is
the friction occurring between the bullet and the barrel and
the classical friction model is speed independent. The other
resistance is provided by the column of air that has to be
quickly displaced as the bullet is going through the barrel.
This resistance will be grouped into the friction resistance
since no measurements were made to isolate this resistance.
For
friction, there is a static and a kinetic friction. The
static friction is a friction that is over come by the
application of certain force (pressure*area). Once the
bullet has started to move, there is a kinetic friction
which is less than the static friction. These frictions
impacts the calculation of the velocity and travel distance.
These parameters (velocity and distance) can not be
calculated until the chamber pressure achieves a certain
level. At this level the bullet moves from the casing and is
forced into the barrel where the rifling ID is smaller than
the bullet diameter. At this point, kinetic friction is
important. Part of the force on the bullet created by the
chamber pressure is used to overcome this kinetic
resistance. This remaining pressure is used for the velocity
and distance calculations.
Data Collection
The pressure, velocity and
distance equations presented in the previous sections are
used with measured data. The first set of data was acquired
from the internet at [10].
The provided pressure curves were manually digitized. Three
other examples are presented that were acquired through the
circuit described above. The examples are for a Remington
Model 510 22LR rifle, a 12 gauge shotgun and a 7x57 mm
Mauser rifle.
A
Tektronix MDO3104 oscilloscope was used to measure and
digitally collect the amplified Wheatstone voltages. The
measured voltages were AC coupled to remove the DC offsets
in the measurements. There are two sources for the DC
offsets. One is from the offset generated by the REF5020 to
shift the signal from 0 volts (since the opamps were single
ended). The other offset is from the contribution of the
finite lead resistance shown in Equation
5. The alternate approach to account for these offset
would be to measure the DC voltage levels before the
cartridge is fired and subtract this level from the time
varying voltage measurements.
The
physical circuit used in the measurements is shown in Figure
4. A nine volt battery was used to supply power to the
circuit. The wires to the right provided measurement points
for the first and second stage amplifiers. The two position
terminal block on the top was were the strain gage wire were
attached.

Figure
4: The physical pcb used in the measurements.
The
static and kinetic friction forces were found using a
numerical downhill simplex optimizer. The optimizer found
the effective forces (pressures) which the calculated
velocities and distances matched measured values. The
measured velocities were provided by the ammunition
manufactures and the distances from the measured barrel
distances. The functional optimized was:
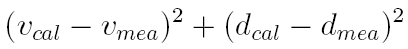
The
pseudo code illustrating how the effective friction forces
were determined is
if(pres\_meas > fric\_static) then
pres\_meas = pres\_meas - fric\_kinetic
continue to determine velocity and distance
end if
where
pres_meas is the chamber pressure found in Equation
14 and the friction values are determined through the
downhill simplex optimizer using the muzzle velocity and the
distance the bullet traveled in the barrel. The friction
forces are then calculated from the psi friction values by
multiplying them with the cross sectional barrel area.
Table
2 contains the various parameters that were used in the
calculations. The provided grain weight values were
converted to slugs for the calculations using a factor of
1\7000.*32.174=4.44*10^-6.
Physical Parameters used for the Numerical Calculations
|
Table 2:
|
|
Parameter |
22LR |
12 Gauge Shotgun |
7x57 Mauser |
|
Barrel ro (inches) |
.383 |
.642 |
.479 |
|
Barrel ri (inches) |
.112 |
.403 |
.225 |
|
Casing ro (inches) |
.112 |
.403 |
.225 |
|
Casing ri (inches) |
.102 |
.370 |
.185 |
|
Bullet OD (inches) |
.224 |
.686 |
.277 |
|
Bullet Mass (grains) |
40 |
492 |
140 |
|
Muzzle Velocity (fps) |
1035 |
1145 |
2660 |
|
Bullet Travel Length (inches) |
24.25 |
31.625 |
21.9375 |
|
Gain |
9880 |
2470 |
24.7 |
|
Young's Modulus (steel) |
30.*10^6 |
30.*10^6 |
30.*10^6 |
|
Young's Modulus (brass) |
16.*10^6 |
|
16.*10^6 |
|
Young's Modulus (LDPE) |
|
.13*10^6 |
|
Internet Data
Measured pressure values for
a 22LR rifle using a 40 grain, .224 caliber bullet in a
24.75'' long barrel can be found at [10]
for two loads. Figure
5 illustrates measured chamber pressure values using RSI
hardware and software for one of the loads. The reference
indicates that the pressure curve has been calibrated but
there is not sufficient information on how it was achieved.
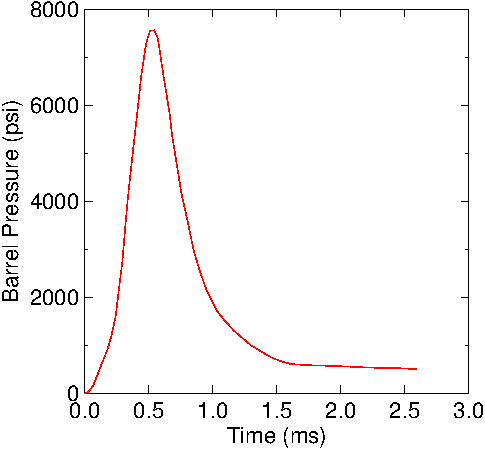
Figure
5 : Measured pressure curve of a 22LR. The barrel pressure
dropped to zero at the end of the traces.
The
calculated velocity and position calculations using this
pressure curve are shown in Figures
6 and
7. Table
3 contains the resulting data.
Generated Data for a 22LR
|
Table 3:
|
|
Parameter |
Data |
|
Measured velocity (fps) |
1035 |
|
Measured length (inches) |
24.25 |
|
Optimized velocity (fps) |
1034 |
|
Optimized lenth (inches) |
23.18 |
|
Static friction (psi) |
39.9 |
|
Kinetic friction (psi) |
27.0 |
|
Static friction (lbs) |
1.57 |
|
Kinetic friction (lbs) |
1.06 |
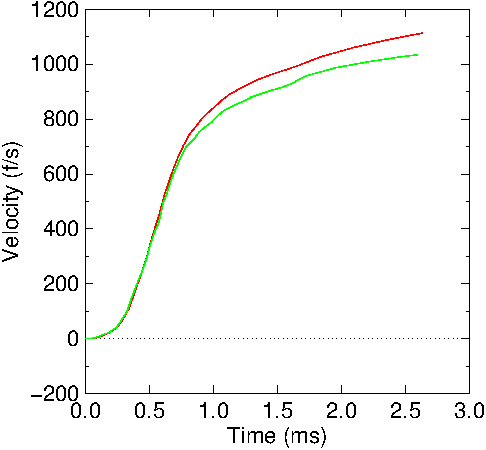
Figure
6: Calculated bullet velocity in the 22LR barrel. Red: no
friction included; Green: friction included.
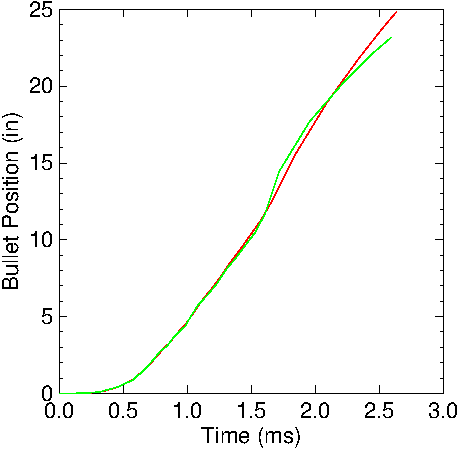
Figure
7: Calculated bullet position in the 22LR barrel. Red: no
friction included; Green: friction included.
Remington Model 510 22LR Rifle
Measurements for a 22LR were performed and Figure
8 illustrates the mounted strain gage.

Figure
8: Strain gage illustration for the Remington Model 510 22LR
rifle.
The
chamber pressures are shown in Figure
9 based upon a circuit gain of 9880. The maximum
measured voltage was 1.74 v which makes the maximum
Wheatstone bridge voltage .17 mv. The receiver prevented the
strain gage to be mounted over the casing of the round.
Hence, no peak chamber pressures could be acquired. Note
that there is a small pressure pulse before the main pulse
around t=.5 ms. All the 2LR measurements had this behavior.
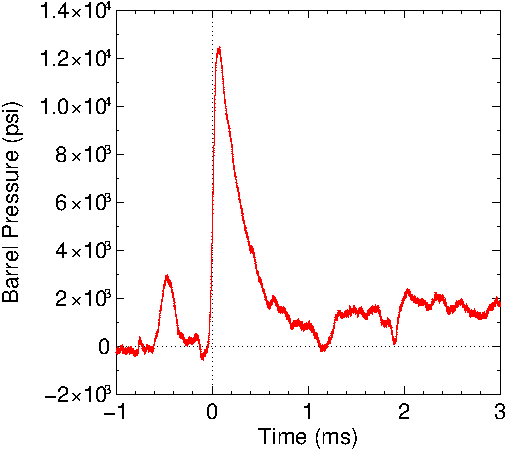
Figure
9 :Chamber pressure for the Remington Model 510 22LR rifle.
12
Gauge Shotgun
The mounted strain gage for a
12 gauge shotgun is illustrated in Figure
10. The shell used was 2.75'' with a shot weight of
1.125 ounces, Winchester AA light target load. The measured
shot velocity using a chronograph was 1145 fps which is also
the manufacture's reported shot velocity.

Figure
10: Strain gage illustration for a 12 gauge shotgun.
The
chamber pressure is shown in Figure
11 based upon a circuit gain of 2470. The calculated
velocity and position calculations using this pressure curve
are shown in Figures
12 and
13. Table
4 contains the resulting data.
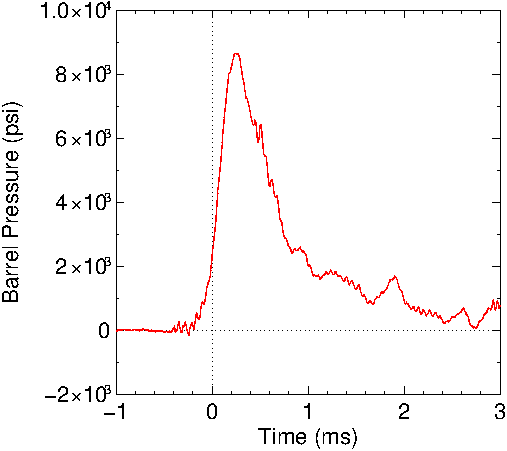
Figure
11: Chamber pressure for the 12 gauge shotgun.
Generated Data for a 12 Gauge Shotgun
|
Table 4:
|
|
Parameter |
Data |
|
Maximum measured voltage (v) |
2.27 |
|
Circuit gain |
2470 |
|
Maximum bridge voltage (mv) |
.91 |
|
Measured velocity (fps) |
1145 |
|
Measured length (inches) |
30.625 |
|
Optimized velocity (fps) |
1145 |
|
Optimized length (inches) |
30.79 |
|
Static friction (psi) |
626 |
|
Kinetic friction (psi) |
55.1 |
|
Static friction (lbs) |
231 |
|
Kinetic friction (lbs) |
20.4 |
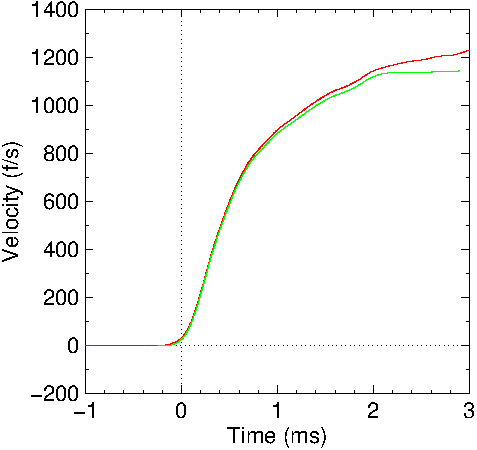
Figure
12: Calculated shot velocity in the shotgun barrel. Red: no
friction included; Green: friction included.
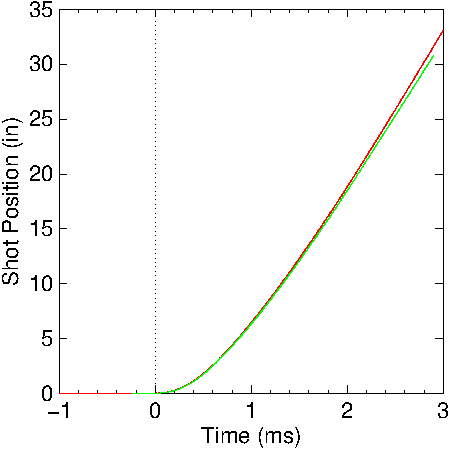
Figure
13: Calculated shot position in the shotgun barrel. Red: no
friction included; Green: friction included.
7x57 mm Mauser Rifle
The mounted strain gauge for
a 7x57 mm Mauser is illustrated in Figure
14. A Federal SP round was used with a reported muzzle
velocity of 2660 fps.

Figure
14: Strain gage illustration for the 7x57 Mauser rifle.
The
chamber pressure is illustrated in Figure
15 with a circuit gain of 24.7. The red curve is
measured data taken from the output of the first stage since
the gain of the second stage was too large for this
measurement. The green curve is post-processed data using a
moving average. Note the pressure spike around .5 ms. This
is when the bullet left the barrel.
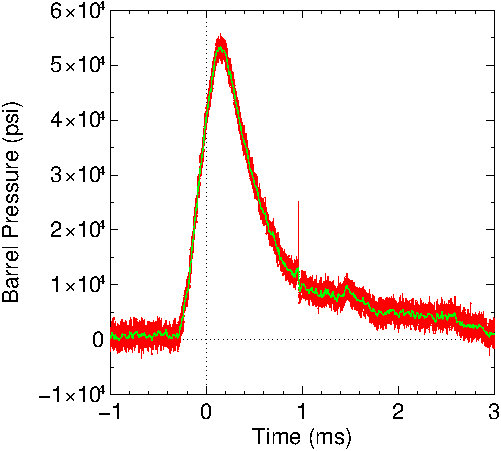
Figure
15: Chamber pressure for the 7x57 Mauser. Note the pressure
spike around .5 ms when the bullet left the barrel. The
green curve is smoothed data using the data in the red
curve.
The
calculated velocity and position calculations using this
pressure curve are shown in Figures
16 and
17. Table
5 contains the resulting data. Comparable results are
obtained using either the raw or smoothed data from Figure
15.
Generated Data for a 7x57mm Mauser
|
Table 5:
|
|
Parameter |
Data |
|
Maximum measured voltage (mv) |
47.2 |
|
Circuit gain |
24.7 |
|
Maximum bridge voltage (mv) |
1.91 |
|
Measured velocity (fps) |
2660 |
|
Measured length (inches) |
21.9375 |
|
Optimized velocity (fps) |
2659 |
|
Optimized length (inches) |
21.1 |
|
Static friction (psi) |
7849 |
|
Kinetic friction (psi) |
1446 |
|
Static friction (lbs) |
497 |
|
Kinetic friction (lbs) |
91.6 |
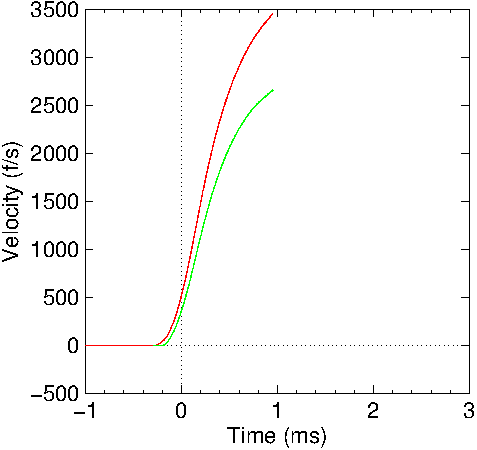
Figure
16: Calculated bullet velocity in the Mauser barrel. Red: no
friction included; Green: friction included.
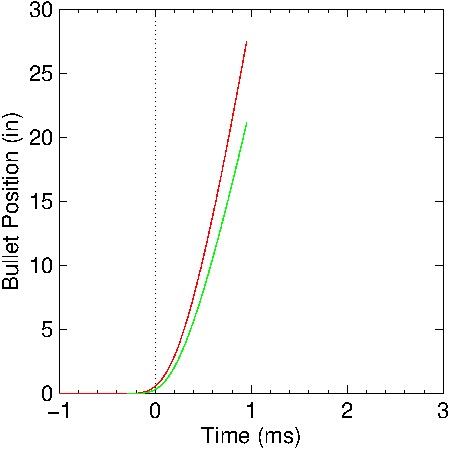
Figure
17: Calculated bullet position in the Mauser barrel. Red: no
friction included; Green: friction included.
Conclusions
The expressions derived and
given here attempt to provide the chamber pressure from an
analytical approach. It is seen that friction is an
important factor in internal ballistics. This measurement
approach can provide data on the static and kinetic friction
for bullet/barrel interactions.
It
was also observed that a better Wheatstone bridge nulling
circuit, gain selection and amplifier configuration would be
useful. Nulling the Wheatstone bridge to an absolute null is
not critical as long as it is not too large to saturate the
high gain amplifier. The residual offset voltage can be
subtracted from the measurement or it can be blocked as was
done in these measurements with the oscilloscope set to an
AC input.
Figure
18 illustrates a possible nulling circuit. The nulling
circuit now includes two trimmers instead of one. These
trimmers provide a coarse and fine adjustment. This
adjustment could be made automatic if a processor was used
in conjunction with digital potentiometers.
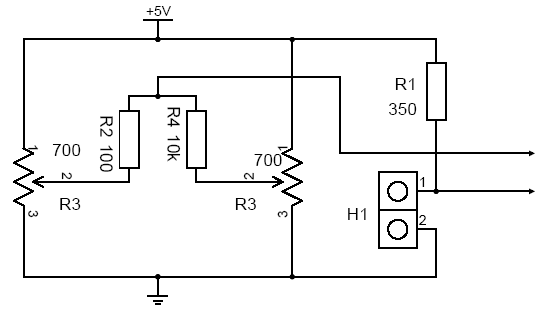
Figure
18: Enhanced nulling circuit for the Wheatstone measurement
circuit.
The
amplifier configuration could also be changed to separate
the amplification from the low pass filtering. The low pass
filtering lessens the appearance of rapid pressure changes
and rapid pressure changes potentially could be missed as
was shown in the Mauser data. The current second amplifier
stage could have its low pass filtering feature removed and
a third stage added to provide low pass filtering with zero
gain. If a third stage is not added for noise reduction,
post processing with a moving average also could be used to
remove the high frequency noise.
The
observed chamber pressure characteristics were as
anticipated except for the chamber pressure not going to
zero once the bullet exited the barrel. This is bothersome
but could be attributed to the thermal heating of the barrel
and strain gage. A second strain gage could have been
attached on the barrel to replace the fixed resistor, R1, in
the Wheatstone bridge. This might have allowed a better,
more natural balance in the nulling circuit. Another
possibility for this behavior might be that the strain gage
was not properly attached to the barrels. A Loctite 401
adhesive was used.
All
the measured and calculated results depend upon the accuracy
of the obtained pressure values. Any measurement has
accuracy concerns. There are many measured parameters in
this effort. The parameters are the physical dimensional
measurements of the barrel and casing, the voltage
measurements and the material properties of Young's modulus.
Another accuracy consideration is that the numerical model
using a simple compound cylinder to approximate a physical
geometry (gun) may have its limitations.
Bibliography
-
Chamber Pressure, https://en.wikipedia.org/wiki/Chamber_pressure
-
Metallic Cartridge Chamber Pressure Measurement, http://www.chuckhawks.com/pressure_measurement.htm
-
Brownell, L.E., York, M., Sinderman, R., Jacob, K.,
Robbins H., "Absolute Chamber Pressure In Center-Fire
Rifles", The University of Michigan, Industry Program of
the College of Engineering, June, 1965, IP-710,
https://deepblue.lib.umich.edu/bitstream/handle/2027.42/3866/
bac6873.0001.001.pdf? sequence=5
-
Recreational Software, Inc., https://www.shootingsoftware.com/pressure.htm
-
Strain Gauges for Chamber Pressure Measurements,
http:www.ktgunsmith.com /straingauge.htm
-
Calculating Barrel Pressure and Projectile Velocity in
Gun Systems, http://closefocusresearch.com/calculating-barrel-pressure-and-projectile-velocity-gun-systems
-
Strain Gauge, https://en.wikipedia.org/wiki/Strain_gaug
-
Quarter Bridge, Half Bridge and Full Wheatstone Bridge
Strain Gauge Load Cell Configurations, Transducer
Techniques, https://www.transducertechniques.com/wheatstone-bridge.aspx
-
Strain Formulas, http://www.mindspring.com/$\sim$sfaber1/strnform3.htm
-
22LR Rifle and Tuner, http://www.varmintal.com/a22lr.htm
-
Thick wall stress formulas. http://www.engineeringtoolbox.com/stress-thick-walled-tube-d_949.html
2017-08-05
|